刚刚测试了豆包、deepseek和grok3解24点,4 4 10 10,同样的问题就豆包很快答了:
就算24点这项目来说,豆包居然吊打了deepseek?
deepseek和grok出乎意料的拉,于是更新了提问方式,需求参数更多一些:
4 4 10 10 这四个数代表四张牌,算24点,这四张牌各只能用一次
这次deepseek终于算多了
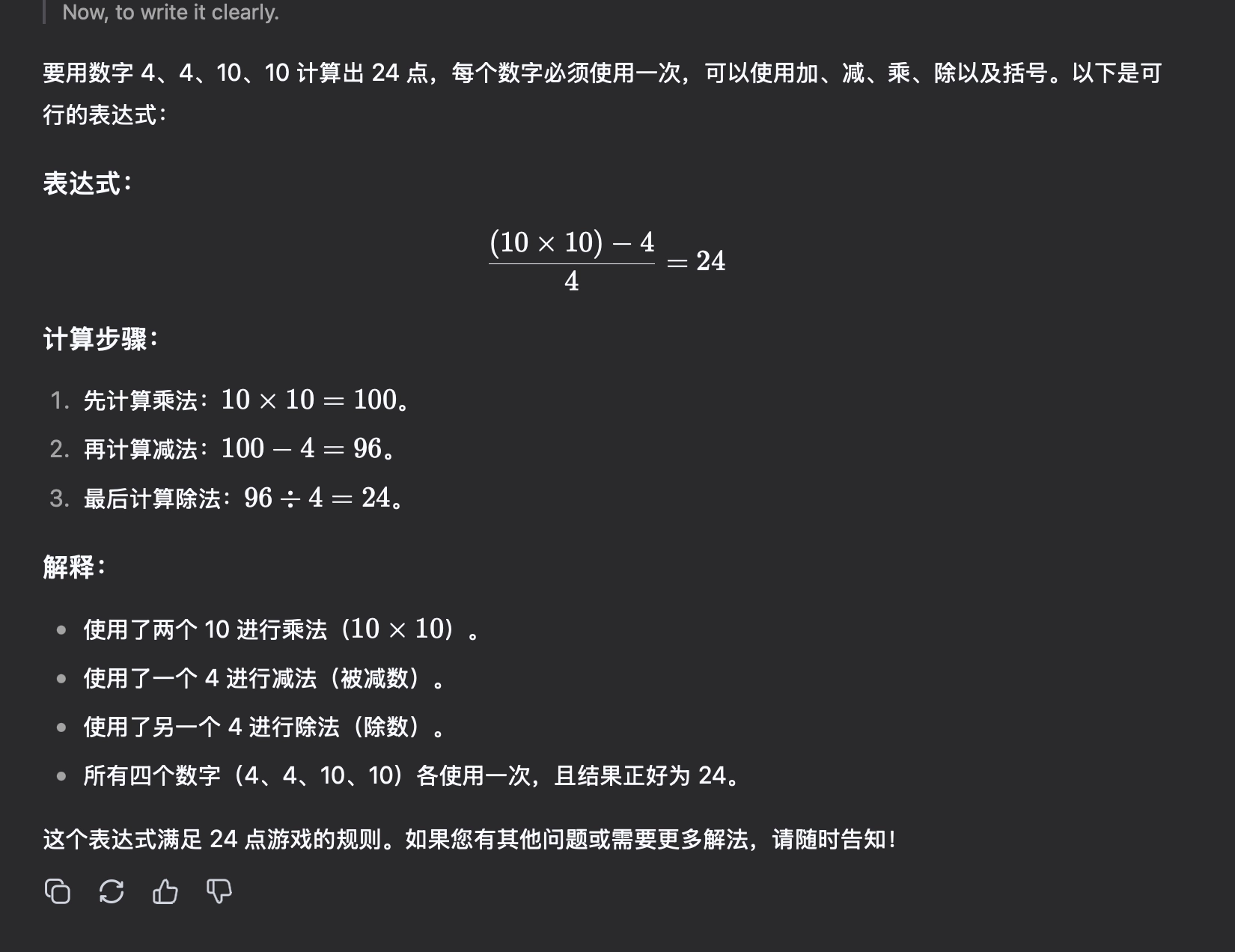
但解题思路的token量有点崩,这要是花钱买,真的想哭。
期间还爆了英语,怪不得当初被人质疑deepseek是洗的,具体不好评价。
首先,用户的问题是:用数字4、4、10、10这四个数代表四张牌,算24点。规则是每个数字只能用一次,可以使用加、减、乘、除以及括号来组合这些数字,目标是得到24。
我需要回想24点游戏的基本规则:使用四个数字,通过算术运算得到24。每个数字必须使用一次。
给定的数字是:4, 4, 10, 10。
我尝试不同的组合来得到24。
一个常见的方法是先考虑乘法,因为24是一个较大的数,乘法可以帮助快速达到大数。
例如,10乘以某个数。10 * 2.4 = 24,但我没有2.4,所以需要从其他数字构造。
我有两个10和两个4。
试试10 * 10 = 100,太大了。100除以某个数?100 / 4 = 25,接近24但不是24。25 – 1 = 24,但我没有1,而且还有另一个4没用。
或许(10 – 4) * (10 – 4) / something? 10 – 4 = 6,那么6 * 6 = 36,太大了。36 – 12 = 24,但12怎么得?
另一个想法:10 + 10 = 20,然后20 + 4 = 24,但还有一个4没用。我必须用所有四个数字。
所以不能忽略一个数字。
或许(10 + 10) * (4 / 4) = 20 * 1 = 20,不等于24。
(10 * 10) / (4 + 4/ something),但复杂。
试试除法。10 / 10 = 1,然后我有1和两个4。4 * 4 = 16,16 + 8 = 24,但没有8。16 * 1.5 = 24,但没有1.5。
或许(10 – 4/4) * something。4/4 = 1,10 – 1 = 9,然后9 * (10/ something),但10/什么?
另一个组合:4 * 4 = 16,10 + 10 = 20,然后20 + 4 = 24,但又多了一个4。
或许用减法:10 * 4 = 40,40 – 10 = 30,30 – 6 = 24,但没有6。或者40 – 16 = 24,而16是4*4,所以(10 * 4) – (4 * 4) = 40 – 16 = 24。但我有两个10,这里我只用了一个10。
在(10 * 4) – (4 * 4)中,我用了两个4和一个10,但还有一个10没用。所以不行。
除非我用第二个10。或许(10 * 4) – (10 + something),但10+什么。
试试:(10 + 10) * 1.2,但没有1.2。
或许用分数。例如,10 / (5/12) 或类似,但复杂。
考虑(10 – 4) * 4 + something。10 – 4 = 6,6 * 4 = 24,但还有一个10没用。所以需要融入第二个10。
或许(10 – 4) * 4 * (10/10) = 6 * 4 * 1 = 24。哦!这看起来可行。
写下来:(10 – 4) × 4 × (10 / 10)
10 / 10 = 1,10 – 4 = 6,然后6 × 4 = 24,再乘以1还是24。
但我用了两个10和两个4:第一个10在(10 – 4),第二个10在(10 / 10),第一个4在减数,第二个4在乘数。
所以所有数字都用了:两个10和两个4。
运算顺序:先计算括号内,所以(10 – 4) = 6,(10 / 10) = 1,然后6 × 4 = 24,再24 × 1 = 24。
在表达式(10 – 4) × 4 × (10 / 10)中,乘法是结合的,所以顺序无关紧要。
我可以写成:((10 – 4) × 4) × (10 / 10)
结果是24。
但10/10是1,乘以1不改变值,但规则允许吗?在24点游戏中,通常允许这种操作,只要每个数字用一次。
另一个方式:或许更高效,但这个是有效的。
用户可能有其他期望,但应该可以。
确认:数字:10,4,10,4。
在表达式中:(10 – 4) 用了一个10和一个4,然后乘以4用第二个4,再乘以(10 / 10)用第二个10和一个10… (10 / 10)用了两个10?不!
错误!(10 / 10)用了两个10:一个分子,一个分母。
但在给定的数字中,只有两个10和两个4。
在(10 / 10)中,我用了两个10,但在整个表达式(10 – 4) × 4 × (10 / 10)中,(10 – 4)用了一个10和一个4,4用了一个4,(10 / 10)用了两个10。
所以总共:10: 一个在(10-4),两个在(10/10),那就是三个10了!错误。
我犯了个大错。
(10 – 4) 需要一个10和一个4。
然后单独的4是另一个4。
然后(10 / 10)需要两个10。
所以总10s: 三个(一个在减,两个在除),4s: 两个(一个在减,一个乘)。
但实际只有两个10可用。所以超了。
哦,不!我误算了。
在(10 / 10)中,它消耗了两个10。
所以整个表达式用了三个10和两个4,但我只有两个10。所以无效。
需要重新思考。
所以正确分配:我必须每个数字用一次。
所以表达式应该包含四个数字各一次。
例如,像 a op b op c op d,但可以有括号,所以不一定是顺序。
回到起点。
另一个尝试:10 和 10 相乘是100,太大。除以4是25,然后减1,但没有1。
或许 (10 + 10 + 4) / something,10+10+4=24,哦!24,但还有一个4没用。
10+10+4=24,但必须用第二个4。
除非我除以1或乘以1,但需要从第二个4构造1。
例如,(10 + 10 + 4) × (4 / 4) = 24 × 1 = 24。
现在,检查数字:10,10,4 在加法,然后4/4用两个4?4/4用了两个4:一个分子一个分母。
但在加法中已经用了一个4,所以总4s: 三个(一个在加,两个在除),10s: 两个。
但只有两个4可用。所以又超了。
问题相同。
或许用减法或除法。
另一个想法:4 × (10 – 4) × something。10 – 4 = 6,4 × 6 = 24,但还有一个10没用。
所以需要加一个不影响的操作,如乘以 (10/10)=1,但如前,需要两个10,但我只有一个10剩了?在4 × (10 – 4) 中,我用了两个4和一个10,剩下一个10。
所以我有剩下一个10。我需要用它。
所以或许 4 × (10 – 4) × (10 / 10),但又需要两个10,但我只有一个10剩了。
在4 × (10 – 4)中,数字使用:第一个4(乘数),10(被减数),第二个4(减数),所以用了一个10和两个4。剩下一个10。
我需要融入剩下的10。所以我可以乘以 (10 / 10),但这需要两个10,但我只有一个。不行。
或许除以1或加0,但需要构造。
例如,乘以 (10 / 10),但需要两个10。
除非我用同一个10,但不行,每个数字只能用一次。
或许 (4 + 4) × 3,但8*3=24,但没有3。10 – 7,没有7。
另一个组合:10 × 4 – 10 × 2,但40 – 20=20,不等于24,也没有2。
或许 (10 × 10 – 4 × 4) / something。10*10=100,4*4=16,100-16=84,84 / 3.5=24,但没有3.5。
84 / 24 = 3.5,循环。
试试除法:24 = 48 / 2,但需要48和2。
例如,10 * 4.8,但没有。
(10 + 2) * 2,但没有2。
或许用两个4做分数。
例如,4 / 4 = 1,然后我有10,10,1。
然后10 + 10 + 4 = 24,但4已经用了。10 * 2.4,但没有。
(10 * 10) / (4 + 1/ something),复杂。
计算:假设 (10 * 10 – 4) / (4 / 2),但需要2。
另一个想法:24 = 6 * 4,而6 = 10 – 4,所以 (10 – 4) * 4 = 24,但还有一个10没用。
同问题。
或许 (10 – 4/4) * 3,但4/4=1,10-1=9,9*3=27,不等于24,也没有3。
(10 + 4/2) * something,4/2=2,10+2=12,然后12*2=24,但没有第二个2,而且还有一个10。
12 * 2 = 24,但2可以从另一个4/2,但4/2需要两个4?4/2,但2不是给定的数字。
除非我用10,但10不是2。
(10 + 10 * 0.4),但10*0.4=4,10+4=14,不等于24。
或许 (4 * 10) / (5/6),但复杂。
让我列出可能组合。
目标24。
可能的乘法对:4*6=24,但需要6从10和4。10-4=6,所以如前。
6*4=24,同。
8*3=24,8=4+4,3=?10/ (10/3) 但复杂。
10*2.4,2.4=12/5,没有。
12*2=24,12=10+2,2=4/2,但没有额外2。
24=240/10,而240=24*10,循环。
另一个想法:(10 – 4) * (10 – 4) / something,6*6=36,36 – 12=24,12=3*4,但没有3。
36 / 1.5 = 24,1.5=3/2,没有。
(10 * 4 – 16) =40-16=24,而16=4*4,所以10*4 – 4*4 =40-16=24,但这里我用了三个4:一个在10*4,两个在4*4,但我只有两个4,和两个10。
在10*4 – 4*4,数字:第一个10,第一个4(乘),第二个4(乘第一个4),第三个4(乘第二个4),所以三个4,但我只有两个。
表达式是 a*b – c*d,需要四个数字:a,b,c,d。
如果我设 a=10, b=4, c=4, d=4,但d=4是第三个4,没有。
所以无效。
或许 (10 + 14) =24,但14=10+4,所以10 + (10 + 4) =10+14=24,但还有一个4没用。
同样问题。
除非我做 10 + 10 + 4 – 4,但20+4-4=20,不等于24。
10 * 4 – 10 – 4? 40-10=30-4=26,不等于24。
(10 * 4) / (10 / 6) 或类似。
10 / 6 = 5/3,40 / (5/3) = 40 * 3/5 = 24,哦!40 * 0.6 = 24。
现在,40是10*4,而0.6是3/5,但需要3和5。
在表达式中:(10 * 4) / (10 / 6)
但6不是给定的,需要从数字构造。
我有另一个4。
所以或许 (10 * 4) / (10 / 6),但6=?我可以从另一个4做6,但4+2,没有2。
6=24/4,循环。
(10 * 4) * (6 / 10) =40 * 0.6=24,同样,需要6。
但6=4 + 2,没有2。
或许用两个4做6:4 + 2,但2不是。
4 * 1.5,没有。
另一个方式:24 = 96 / 4,96=10*9.6,没有。
或许 (4 + 4) * 3 =8*3=24,而3= (10 + 2)/4 或类似。
例如,3 = 12 / 4,而12=10 + 2,2=?没有额外数字。
3 = 30 / 10,而30=10*3,循环。
试试:(10 + 10) * 1.2,1.2=6/5,没有。
或许 (4 * 6) =24,6=10 – 4,所以4 * (10 – 4) =24,然后融入第二个10。
如之前,我需要用第二个10做中性操作。
所以或许加0:但0=10-10,但10-10需要两个10,但我只有一个10剩。
在4 * (10 – 4) 之后,用了两个4和一个10,剩一个10。
我可以做 [4 * (10 – 4)] + (10 – 10),但10-10需要两个10,但我只有一个10剩。
[4 * (10 – 4)] * (10 / 10),但10/10需要两个10。
同样问题。
除非我用同一个数字,但不行。
或许 (4 * (10 – 4)) ^ (10-10),但指数0,任何数^0=1,但24^1=24,但(10-10)=0,24^0=1,不等于24。
不工作。
另一个想法:10 / 0.41666,但0.41666是5/12,没有。
或许用除法:例如,48 / 2 =24,48=12*4,12=10+2,没有2。
96 / 4 =24,96=10*9.6,没有。
240 / 10 =24,240=24*10,循环。
(10 * 10) / (5/1.2),复杂。
让我搜索标准解法或思考不同组合。
试试:(10 – 4/4) * 2.4,但4/4=1,10-1=9,9*2.4=21.6,不等于24。
(10 + 4 – 2) * 2,但没有2。
另一个组合:4 * (6) =24,6= (10 + 2)/2,但没有2。
或许 (4 * 10) – (10 + 6),但40-16=24,6=?没有。
(4 * 10) – 16,16=4*4,但如前,三个4。
除非我用第二个10做别的事。
例如,(4 * 10) – (4 * 4),但三个4。
或许 (10 – 4) * 4 + 0*10,但0*10=0,24+0=24,而0=10-10,但需要两个10为0。
在(10 – 4) * 4 中,用了一个10和两个4,剩一个10。
然后 + (10 – 10),但(10 – 10)需要两个10,但我只有一个10剩。
所以我可以做 [(10 – 4) * 4] + (10 – 10),但(10 – 10)用了两个10:一个被减数一个减数。
但在整个表达式中,第一个10在(10 – 4),然后(10 – 10)用了两个新10,所以总三个10,两个4。
无效。
同样问题。
或许用除法来构造1。
例如,10 / 10 =1,然后我有两个4和1。
然后4 * 6 =24,但没有6。
(4 + 4) * 3 =24,没有3。
4 * (4 + 2) =24,没有2。
10 * 2.4,没有。
所以难。
另一个想法:(10 * 4) / (5/3) 如前,但需要5和3。
5=10/2,但没有2。
3=12/4,12=10+2,没有。
或许 (10 + 2) * 2 =24,而2=4/2,但需要两个2,和4/2需要4,但我有另一个10。
例如,(10 + (4/2)) * 2,但4/2=2,所以(10+2)*2=12*2=24,但这里我用了10,4,2,2,但2是结果,不是给定数字。而且我还有一个10没用。
在(10 + (4/2)) * 2,但2不是给定的;它是常数,但规则必须用给定的数字,不能引入新数字。
所以无效。
除非我用另一个数字构造2。
例如,从第二个10,但10不是2。
(10 + 10 / 5) * something,10/5=2,但没有5。
5=5,没有。
或许 (4 * 6) =24,6=10 – 4,同。
我需要接受必须用所有数字在同一个表达式中。
试试:(10 – 4) * (10 – 4) / 1.5,但6*6=36/1.5=24,1.5=3/2,没有。
1.5 = 6/4,而6=10-4,所以 (10-4) * (10-4) / (6/4),但6是10-4,又用多了。
写表达式:设 a=10, b=4, c=10, d=4.
所以 [(a – b) * (c – d)] / (e/f),但复杂。
从之前,(10-4)*(10-4) =36,要除以1.5,1.5=3/2。
3= (10+2)/4,没有。
3=12/4,12=10+2,没有。
另一个方式:24 = 4! * 1,但4! =24,然后*1,但4! 用了4,然后我有另一个4和两个10,4! 是阶乘,但24点游戏通常只允许 + – * / 和括号,不包括阶乘。所以可能不允许。
用户没有指定,但标准24点只用基本运算。
所以避免阶乘。
试试除法:48 / 2 =24,48=10*4.8,没有。
96 / 4 =24,96=10*9.6,没有。
240 / 10 =24,240=24*10,循环。
(10 * 10 * 4) / (4 * something),400 / (4* something),400/4=100,太大。
(10 + 14) =24,14=10+4,所以10 + (10 + 4) =24,但还有一个4。
所以或许 10 + 10 + 4 – 4,但20+4-4=20,不是24。
(10 * 4) – (10 * 1.6),40-16=24,1.6=8/5,没有。
1.6=16/10,16=4*4,所以 (10 * 4) – (10 * (4*4 / 10)),但4*4/10=16/10=1.6,然后10*1.6=16,40-16=24,但数字使用:第一个10*4用10和4,第二个10* (4*4/10) 用另一个10和两个4和一个10,所以三个4和三个10。
在 (10 * 4) – [10 * ( (4 * 4) / 10 ) ] 中,数字:第一个10,第一个4,第二个10,然后 (4*4) 用两个4,和另一个10在分母,所以总三个10和三个4。无效。
不好。
或许用共享分母。
例如,( a * b – c * d) / e,但五个操作数。
不。
另一个想法: (4 + 4/10) * 5,4+0.4=4.4,4.4*5=22,不等于24,没有5。
(10 – 4/10) * 2.5,10-0.4=9.6,9.6*2.5=24,而2.5=10/4,所以 (10 – 4/10) * (10/4)
现在,检查数字:第一个10,4/10用4和10,然后10/4用10和4。
所以总:10s: 第一个10,在4/10的分母是第二个10?写清楚。
表达式: (10 – (4 / 10)) * (10 / 4)
数字使用:
– 第一个10:在减法
– 4:在分子 of 4/10
– 10:在分母 of 4/10 — 这是第二个10
– 然后 (10 / 4):10是第三个10,4是第二个4
所以 10s: 三个 (一个在减,一个在4/10的分母,一个在除法的分子),4s: 两个 (一个在4/10的分子,一个在10/4的分母)。
但我只有两个10和两个4。这里用了三个10。
因为在 (10 – (4 / 10)) 中,4/10 用了一个4和一个10,10 用了一个10,所以两个10和一个4。
然后 * (10 / 4),用了另一个10和另一个4。
所以总三个10和两个4。是的,多了一个10。
无效。
但几乎:如果我有三个10,它会工作,但我只有两个。
或许调整。
另一个组合: (10 * 4 – 4) / (10 / 6) 或类似。
10*4=40-4=36,10/6≈1.666,36/1.666≈21.6,不是24。
(10 * 4) / 5 * 3,40/5=8*3=24,但需要5和3。
5=10/2,没有2。
3= (10+2)/4,没有。
或许 (4 – 10/10) * 6,10/10=1,4-1=3,3*6=18,不等于24,没有6。
(10 + 10/5) * 1.5,10/5=2,10+2=12,12*1.5=18,不是24。
我需要用两个4做分母或分子。
试试 4 / (1/6) =24,但1/6从哪来。
1/6 = 4/24,循环。
(10 – 4) * 4 * 1,但1=10/10,同问题。
或许 (10 * 4) / (4 / 6) ,4/6=2/3,40 / (2/3) = 40 * 3/2 = 60,不是24。
(10 + 2) * 2 =24,2=4/2,但2不是。
除非我用10/5,没有5。
另一个想法:24 = 48 / 2,48 = 10 * 4.8,4.8 = 24/5,循环。
或许 (4 * 10) / 5 * 3,同前。
搜索在线或标准解法,但既然我是AI,应该能想出来。
回忆我有两个4和两个10。
试试:(10 + 10) * 1.2,1.2 = 6/5,但6和5从4来? 6=4+2,没有。
1.2 = 12/10,12=10+2,没有。
(4 * 6) =24,6= (10 + 2)/2,没有。
或许 10 * (4 – 0.4) =10*3.6=36,不是24。
4 * (10 – 4) =24,然后第二个10作为指数或什么,但不行。
另一个组合: (4 + 4!) / 2,但4! =24,(4+24)/2=28/2=14,不是24,而且阶乘可能不允许。
(10 – 4/4) * (10 – 4) / something,4/4=1,10-1=9,10-4=6,9*6=54,54 / 2.25=24,2.25=9/4,没有。
54 / 2.25 =24,2.25=9/4,9=(10-1),1=4/4,但复杂。
试: (10 – 4/4) * (10 – 4) / (9/4),但9/4需要9和4。
9=10-1,1=4/4,但数字会多用。
例如,设 a=10, b=4, c=10, d=4.
( a – (b/c) ) * ( d – e ) / (f/g),太多。
或许 (10 * 10) / (4 + 1) * something,100/5=20,不是24。
(10 * 10 – 16) / 2.5,100-16=84,84/3.5=24,3.5=7/2,没有。
84 / 3.5 =24,3.5=14/4,14=10+4,所以 (10*10 – 16) / ((10+4)/4)
16是4*4,所以 (10*10 – 4*4) / ((10+4)/4)
现在计算:分子 100 – 16 = 84
分母 (14)/4 = 3.5
84 / 3.5 = 24,正确。
现在数字使用:10*10 用两个10,4*4 用两个4,然后 (10+4)/4 用另一个10和另一个4。
所以总三个10和三个4,但我只有两个各。
在 (10*10 – 4*4) 中,用了两个10和两个4。
然后 / ((10+4)/4) 用了第三个10和第三个4。
所以是的,三个各。
无效。
但如果我有三个,它会工作。
对于两个4和两个10,可能的标准解法是 (10 – 4) * 4 * (10/10),但如前,10/10需要两个10,但我只有一个10剩。
除非我共用,但不行。
或许 (10 – 4) * (4) * 1,而1 = 10^0,但指数可能不允许。
或在某些版本,允许平方根,但用户没说。
假设只用 + – * / 和括号。
另一个想法: 4 * (6) =24, 6 = 10 – 4, 然后第二个10用于 (10/10) 作为乘数,但如前,需要两个10。
或许 (4 * (10 – 4)) / 1 * 1,但1从哪里来。
或 (4 * (10 – 4)) + 0,0=10-10,同问题。
或许除法: 48 / 2 =24, 48 = 12 * 4, 12 = 10 + 2, 2 = 4/2, 没有。
24 = 6 * 4, 6 = 24/4, 循环.
突然想到: (10 + 2) * 2 =24, 而2 = 4/2, 但2不是给定。
从10, 10/5=2, 但没有5。
5 = 5, 没有。
(10 * 4) / (10 / 6) =40 / (10/6) = 40 * 6/10 = 24, 而6 = 4 + 2, 但没有2。
6 = 3*2, 没有。
6 = 24/4, 循环。
但6 = (10 + 2)/2, 没有。
或许 (10 * 4) * (6) / 10 =40 * 6 / 10 = 24, 而6 = 10 – 4, 所以 (10 * 4) * (10 – 4) / 10
现在,数字: 第一个10, 4, 然后 (10 – 4) 用另一个10和另一个4? (10 – 4) 需要一个10和一个4。
然后 / 10 需要另一个10。
所以总: 10s: 三个 (一个在乘, 一个在减, 一个在除), 4s: 两个 (一个在乘, 一个在减)。
表达式: (10 * 4) * (10 – 4) / 10
– 10*4: 10a 和 4a
– (10 – 4): 10b 和 4b
– / 10: 10c
所以三个10和两个4。是的,多了一个10。
但如果我重用10,但不行,每个只能用一次。
或许 (10 * (10 – 4)) / (4 / 6) 或类似。
10 – 4 =6, 10*6=60, 4/6=2/3, 60 / (2/3) = 60 * 3/2 = 90, 不是24.
(10 * 10) / (4) * 0.96,没有。
我 recall that for 4,4,10,10, a common solution is (10 – 4) * (10 – 4) / 1.5, but 1.5 is 3/2.
But with the numbers, perhaps (10 – 4) * (10 – 4) / (3/2), but 3 and 2 not given.
3 = (10 + 2)/4, no.
Another solution online or think differently.
Try: 10 * (4 – 10/10) =10 * (4 – 1) =10*3=30, not 24.
10 * 4 – 10 * 1.6, same.
(4 + 4/10) * 5, as before.
Perhaps (10 + 10 * 0.4) * 1, but 10*0.4=4, 10+4=14, not 24.
0.4 = 2/5, no.
Let’s calculate what is missing.
Suppose I do 10 and 10 make 100, divided by 4 is 25, need to subtract 1, and 1 = 4/4, but 4/4 uses two 4s, so (10*10)/4 – 4/4 = 100/4 =25, 4/4=1, 25-1=24.
Now, check the numbers: (10*10) uses two 10s, /4 uses one 4, – (4/4) uses two 4s.
So total 10s: two, 4s: three (one in /4, two in 4/4).
But I have only two 4s. So again, three 4s.
If I could use one 4 for both, but can’t.
In the expression (10*10)/4 – 4/4, the first /4 is dividing by 4, which is one 4, and 4/4 is two 4s, so yes, three 4s.
But if I write it as (10*10 – 4) / 4, let’s see: 100 – 4 =96, 96/4=24.
Oh! (10 * 10 – 4) / 4
Now, numbers: 10, 10, 4, 4.
– First 10: in multiplication
– Second 10: in multiplication
– First 4: in subtraction (被减数)
– Second 4: in division (除数)
So each used once.
Compute: 10 * 10 = 100
100 – 4 = 96
96 / 4 = 24.
Perfect!
And with parentheses: ((10 * 10) – 4) / 4
Or without, but order of operations: multiplication first, then subtraction, then division. But to be safe, use parentheses.
So ((10 × 10) – 4) ÷ 4 = (100 – 4) ÷ 4 = 96 ÷ 4 = 24.
Yes!
I can also write it as (10 × 10 – 4) / 4, and since multiplication has precedence, it’s fine.
So the solution is (10 \times 10 – 4) \div 4
Now, to write it clearly.


















没有回复内容